BOTTIGLIA DI KLEIN (OTRE DI KLEIN )
Come il NASTRO DI MÖBIUS anche la BOTTIGLIA DI KLEIN è una superficie topologica.
La topologia è un’area della matematica che studia la deformazione plastica dei corpi geometrici e le proprietà che si mantengono invariate nella trasformazione .
La BOTTIGLIA DI KLEIN è stata descritta per la prima volta nel 1882 da Felix Klein (1849-1925) professore all'Università di Gottingen, uno dei più importanti matematici tedeschi dell’epoca.

E' una superficie topologica aperta non-orientabile, cioè una superficie dove non c'è distinzione fra "interno" ed "esterno”.
Si immagini una bottiglia con un buco sul fondo. Ora si estenda il collo della bottiglia, curvandolo su se stesso, fino ad inserirlo lateralmente all'interno di questa.. Infine, si colleghi il collo con il buco in fondo.
Diversamente da un bicchiere, questo oggetto non ha "bordi" dove la superficie termina bruscamente. Diversamente da un pallone, una mosca potrebbe andare dall'interno all'esterno senza attraversare la superficie (quindi non esiste realmente un "dentro" e un "fuori").
Dividendo la bottiglia di Klein lungo il suo piano di simmetria si ottengono due nastri di Möbius.

Questo schema descrive la costruzione di una superficie topologicamente equivalente ad una bottiglia di Klein con un foro (slip di Möbius).
Due nastri a T uniti tra loro alle estremità creano una superficie continua tra interno ed esterno.
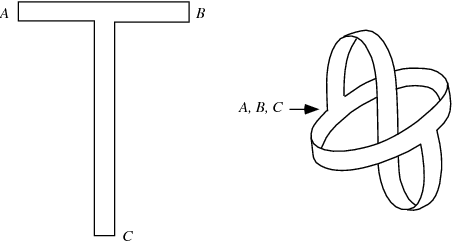
Questo è un bottone Klein, anch'esso equivalente a una bottiglia di Klein con un foro.
Un bel testo di P. Odifreddi in cui spiega che...
Vuoi comperare una bottiglia di Klein in vetro?
Visita il sito: http://www.kleinbottle.com/

