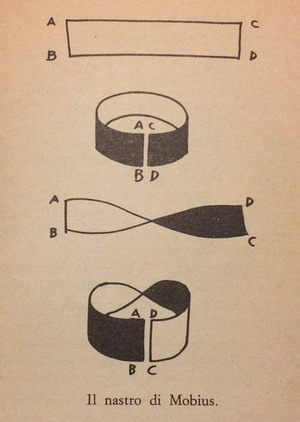
NASTRO DI MÖBIUS

E’ una forma plastica ad anello con una sola superficie continua .

Deve il suo nome al matematico e astronomo August Ferdinand Möbius (1790-1868) che fu il primo a considerare queste particolari superfici, appartenenti alla geometria topologica (dal greco topos e logos= studio dei luoghi).

La topologia è un’area della matematica che studia la deformazione plastica dei corpi geometrici e in particolare i concetti di continuità cioè le caratteristiche e le proprietà che si mantengono invariate nella trasformazione . Si potrebbe dire che la topologia è autorizzata a piegare, allungare , attorcigliare o restringere gli elementi, ma senza romperli o segmentarli .

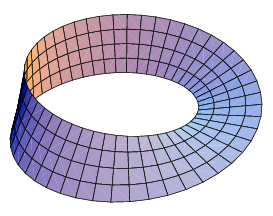
Le superfici geometriche che nella vita quotidiana siamo abituati ad osservare, hanno sempre due facce, una interna ed una esterna, un lato superiore e uno inferiore.Nel caso del nastro di Möbius, invece, tale principio viene a mancare: esiste un solo lato e un solo bordo. “ E' possibile che un corpo plastico abbia una superficie sola, non abbia dentro e fuori, e sia limitato da una sola banda? " Bruno Munari nel libro “Arte come mestiere"( Laterza 1970) spiega con un esempio pratico questo paradosso.
Un nastro di Möbius può essere realizzato partendo da una striscia rettangolare unendo i lati corti dopo aver impresso ad uno di essi mezzo giro di torsione (180°). Se si percorre il nastro con una matita, partendo da un punto casuale, si noterà che la traccia si snoda sull'intera superficie del nastro, che è quindi unica.

 Forme matematiche e topologiche hanno ispirato molti artisti, come Max Bill con gli “endless Ribbon" del 1936, e come il famoso grafico olandese Maurits Cornelius Escher, con le visionarie elaborazioni grafiche.

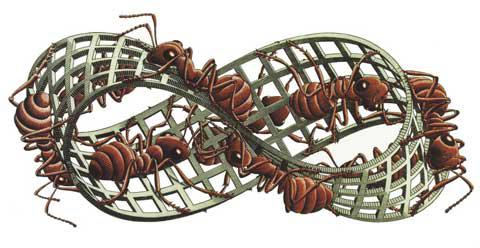Max Bill: “endless Ribbon"	Mauritius Escher: nastro di Moebius

Clifford A. Pickover
"Il nastro di Möbius" Apogeo 2006
Questo libro analizza approfonditamente il nastro di Moebius, nei vari aspetti scientifici, letterari, artistici, ludici.
Ricco di immagini esplicative e con molti riferimenti bibliografici e sitografici.